Math In Society: Loan Payments

Section 2.4 Loan Payments

Objectives

Students will be able to:

Use a spreadsheet and/or formula to calculate the payment amount for student loans, car loans, paying off credit cards and mortgage loans
Calculate the total paid over the life of a loan, amount of interest paid, and the percentage of the total amount paid in interest
Determine when to use each formula in the financial math chapter

In the last section, you learned about savings plans. In this section, you will learn about conventional loans (also called amortized loans or installment loans). Examples include student loans, car loans and home mortgages. These techniques do not apply to payday loans, add-on loans, or other loan types where the interest is calculated up front. In this section we will also briefly cover credit cards. There is a more thorough chapter on credit cards available as an optional chapter.

Figure 2.4.1. Alternative Video Lessons

Subsection 2.4.1 Installment Loans

Installment loans are also called amortized loans. They are designed so that the payment amount remains the same over the life (term) of the loan. In order for that amount to remain constant, the amount of money going towards paying the principal (amount owed) and towards the interest will vary. At the beginning of the loan, the amount owed is the largest. So, at the beginning the amount of interest charged will also be the largest. As the loan gets repaid the amount owed is reduced and therefore the interest is reduced. Therefore, at the beginning of an installment loan payments go mostly towards the interest, towards the end the payments are going mostly towards the principal.

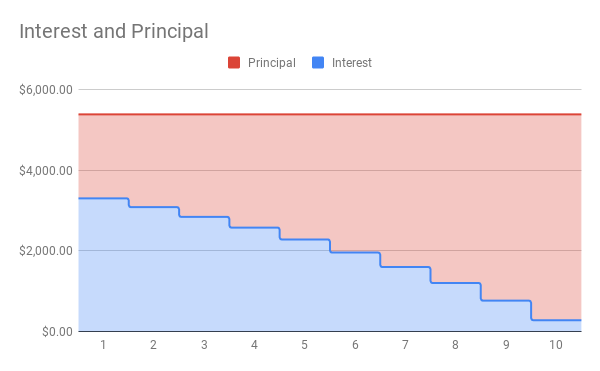
A graph that shows how most of the payment goes to interest at the beginning of the loan and that decreases over time until the end of the loan when most of the payment goes toward the principal.

This is a graph of the interest and principal paid on a loan of $34,000 at 10% APR. Each year $5,391.72 was paid in total. In the first year, $3,305.92 was applied to the interest and $2,085.80 was applied to the principal. In the last year of the loan, only $281.04 was applied to the interest and $5,110.68 was applied to the principal. Over 5 years, a total of $53,917.2 was paid for a loan of $34,000.

Subsection 2.4.2 Loan Formulas

In a savings plan, you start with nothing, put money into an account once or on a regular basis, and have a larger balance at the end. Loans work in reverse. You start with a balance owed, make payments and the future value is zero when the loan is paid off.

We will continue to use the same spreadsheet formulas. The ones that are most useful for loans are =PV and =PMT. We will look at how the inputs change for a loan.

Spreadsheet Formulas.

=PV(rate per period, number of periods, payment amount, future value)

=PMT(rate per period, number of periods, present value, future value)

rate per period: is the interest rate per compounding period, $r/n$
number of periods: is the total number of periods, $n*t$
payment amount: is the amount of regular payments, $d$
present value: is the amount deposited or principal, $P$
future value: is the amount you want in the future, 0 for a loan

These two formulas correspond to the formulas below. The formula for loans is derived in a similar way that we did for savings plans, but notice they have negative exponents. The details are omitted here.

Loan Formulas.

\begin{equation*} P=\frac{d\left(1-\left(1+\frac{r}{n}\right)^{-nt}\right)}{\left(\frac{r}{n}\right)} \text{ or } d=\frac{P\left(\frac{r}{n}\right)}{\left(1-\left(1+\frac{r}{n}\right)^{-nt}\right)} \end{equation*}

$P$: is the balance in the account at the beginning (the principal, or amount of the loan).
$d$: is your loan payment (your monthly payment, annual payment, etc.)
$r$: is the annual interest rate in decimal form
$n$: is the number of compounding periods in one year
$t$: is the length of the loan, in years

Like before, the compounding frequency is not always explicitly given, but is determined by how often you make payments

Example 2.4.2.

Teresa wants to buy a car that costs $15,000. She has $3,000 saved for the car and plans to finance the rest. She found a 3-year loan at 2.75% APR and a 5-year loan at 4% APR. How much will her monthly car payment be for each loan and how do these loans compare to each other.

To use a spreadsheet, we use the =PMT formula. For a loan, the loan amount is the present value and the future value is 0, indicating that the loan will be paid off. Teresa is making a down payment, so we also need to subtract that from the cost of the car to find the loan amount:

$\$15{,}000 – \$3{,}000 = \$12{,}000$

Her loan amount is $12,000. For the 3-year loan at 2.75% APR, we enter:

=PMT(0.0275/12, 12*3, 12000, 0)

and get a result of $347.65.

An image of the spreadsheet showing the formula used and the result.

For the formula, we use the one solved for $d\text{:}$

$r=.0275\text{,}$ for 2.75% annual rate

$n=12\text{,}$ monthly payments

$t=3\text{,}$ for 3 years

$P=12000\text{,}$ since she can pay $3,000 of the $15,000

\begin{align*} d\amp=\frac{P\left(\frac{r}{n}\right)}{\left(1-\left(1+\frac{r}{n}\right)^{-nt}\right)}\\ \amp=\frac{12000\left(\frac{0.0275}{12}\right)}{\left(1-\left(1+\frac{0.0275}{12}\right)^{-12\cdot 3}\right)}\\ \amp\approx\$347.65 \end{align*}

Teresa’s car payment would be $347.65.

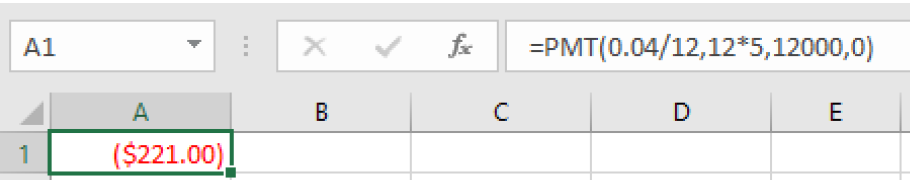
Now for the 5-year loan at 4% APR, we enter:

=PMT(0.04/12, 12*5, 12000, 0)

and we get $221.00.

To use the formula, we have:

$r=.04\text{,}$ for 4% annual rate

$n=12\text{,}$ monthly payments

$t=5\text{,}$ for 5 years

$P=12000\text{,}$ the loan amount

\begin{align*} d\amp=\frac{P\left(\frac{r}{n}\right)}{\left(1-\left(1+\frac{r}{n}\right)^{-nt}\right)}\\ \amp=\frac{12000\left(\frac{0.04}{12}\right)}{\left(1-\left(1+\frac{0.04}{12}\right)^{-12\cdot 3}\right)}\\ \amp\approx\$221.00 \end{align*}

Now let’s compare the loans by finding out how much Teresa would pay in interest for each loan.

For the 3-year loan at 2.75% APR, her payments would total:

\begin{equation*} \$347.65(12)(3)=\$12{,}515.40\text{.} \end{equation*}

Her interest would be $515.40.

For the 5-year loan at 4% APR, her payments would total:

\begin{equation*} \$221.00(12)(5)=\$13{,}260.00\text{.} \end{equation*}

Her interest would be $1,260.00.

There are two main differences between these two loans: the monthly payments and the total paid over the life of the loans. The first loan has a higher monthly payment by $126.65 per month. However, she would pay $744.60 less in interest.

In addition to loan payments, we can calculate the amount of loan we can afford given a monthly payment. Let’s look at that in the next example.

Example 2.4.3.

You can afford $200 per month as a car payment. If you can get an auto loan at 3% APR for 60 months (5 years), how expensive of a car can you afford? In other words, what amount loan can you pay off with $200 per month?

Solution.

To use a spreadsheet for this problem, we use the =PV formula because we want to know the present value, which is the value of the loan right now. We enter

=PV(0.03/12, 12*5, 200,0)

which gives $11,130.47.

To use a formula, we are looking for $P\text{,}$ the starting amount of the loan.

$d=\$200\text{,}$ the monthly loan payment

$r=0.03\text{,}$ 3% annual rate

$n=12\text{,}$ since we’re doing monthly payments, we’ll compound monthly

$t=5\text{,}$ since we’re making monthly payments for 5 years

\begin{align*} P\amp=\frac{d\left(1-\left(1+\frac{r}{n}\right)^{-nt}\right)}{\frac{r}{n}}\\ \amp=\frac{200\left(1-\left(1+\frac{0.03}{12}\right)^{-12\cdot 5}\right)}{\frac{0.03}{12}}\\ \amp=\frac{200(1-(1.0025)^{-60})}{0.0025}\\ \amp\approx\$11{,}130.47 \end{align*}

You can afford a maximum loan of $11,130.47. If you have a down payment you can add that to get the value of the car you can buy. If there are any closing costs for the loan you also need to take that into consideration.

To find the amount of interest you will pay for this loan, calculate the total of all your payments.

$\$200(5)(12)=\$12{,}000$

Then take the difference between the total payments and the loan amount.

$\$12{,}000-\$11{,}130.47=\$869.53$

In this case, you would be paying $869.53 in interest.

So far, we have looked at car loans. Student loans and home mortgages are calculated in the same way. Here is an example of a mortgage payment.

Example 2.4.4.

You want to take out a $140,000 mortgage (home loan). The interest rate on the loan is 6%, and the loan is for 30 years. How much will your monthly payments be? What percentage of your total payments will go towards interest?

Solution.

To use a spreadsheet for this problem, we use the =PMT formula because we want to know the payment amount. The amount of the loan is the present value and to pay off the loan the future value is 0. We enter

=PMT(0.06/12, 12*30, 140000,0)

which gives us $839.37.

To use the formula, we have:

$r=0.06\text{,}$ 6% annual rate

$n=12\text{,}$ since we’re paying monthly

$t=30\text{,}$ 30 years

$P=\$140{,}000\text{,}$ the starting loan amount

In this case, we’re going to use the equation that is solved for $d\text{.}$

\begin{align*} d\amp=\frac{P\left(\frac{r}{n}\right)}{\left(1-\left(1+\frac{r}{n}\right)^{-nt}\right)}\\ \amp=\frac{140000\left(\frac{0.06}{12}\right)}{\left(1-\left(1+\frac{0.06}{12}\right)^{-12\cdot 30}\right)}\\ \amp=\frac{700}{(1-(1.005)^{-360})}\\ \amp\approx\$839.37 \end{align*}

You would make payments of $839.37 per month for 30 years. To find out what percentage of the total will go towards interest, we need to total up all of the payments.

\begin{equation*} \$839.37(30)(12)=\$302{,}173.20 \end{equation*}

Then take the difference between the total payments and the loan amount.

\begin{equation*} \$302{,}173.20-\$140{,}000=\$162{,}173.20 \end{equation*}

In this case, you would be paying $162,173.20 in interest over the life of the loan. To find the percentage, we divide the interest by the total amount paid.

\begin{equation*} \frac{\$162{,}173.20}{\$302{,}173.20} \approx 0.5367 \end{equation*}

About 53.7% of the total is being paid towards interest.

Subsection 2.4.3 Remaining Loan Balance

With loans, it is often desirable to determine what the remaining loan balance will be after some number of years. For example, if you purchase a home and plan to sell it in five years, you might want to know how much of the loan balance you will have paid off and how much you will have to pay from the sale.

To determine the remaining loan balance after some number of years, we first need to calculate the payment amount, if we don’t already know it. Remember that only a portion of your loan payments go towards the loan balance; a portion is going to go towards interest. For example, if your payments were $1,000 a month, after a year you will not have paid off $12,000 of the loan balance.

To determine the remaining loan balance, we can think “how much loan will these loan payments be able to pay off in the remaining time on the loan?”

Example 2.4.5.

If a 30-year mortgage at an interest rate of 6% APR has payments of $1,000 a month, what will the loan balance be in 5 years?

Solution.

To determine this, we need to think backwards. We are looking for the amount of the loan that can be paid off by $1,000 per month in the remaining 25 years. In other words, we’re looking for $P$ when:

$d=\$1{,}000\text{,}$ for the monthly loan payment

$r=0.06\text{,}$ for 6% annual rate

$n=12\text{,}$ since we’re doing monthly payments, we’ll compound monthly

$t=25\text{,}$ since we’d be making monthly payments for 25 more years

To use a spreadsheet for this problem, we use the =PV formula because we want to know what the present value would be at the time you want to sell in 5 years. We enter:

=PV(0.06/12, 12*25, 1000,0)

which gives us $155,206.86.

To check this with the formula we have:

\begin{align*} P\amp=\frac{1000\left(1-\left(1+\frac{0.06}{12}\right)^{-12\cdot 25}\right)}{\frac{0.06}{12}}\\ \amp=\frac{1000(1-(1.005)^{-300})}{0.005}\\ \amp\approx\$155{,}206.86 \end{align*}

The loan balance with 25 years remaining on the loan will be $155,206.86

Sometimes answering remaining balance questions requires two steps, both of which we have done in this section:

Calculate the monthly payment on the loan
Calculate the remaining loan balance based on the remaining time on the loan

Subsection 2.4.4 Credit Cards

Credit cards are useful to many people. They can be used to build a credit score, as a short-term loan and as an alternative to physical cash. It is highly advisable to fully pay off a credit card each month because the interest rates are much higher than the conventional installment loans we discussed earlier. There can also be many expensive fees applied when carrying a balance. Because of these higher rates, it can be very easy to get into a lot of debt quickly.

Credit cards are a common source of loan money, and therefore a common source of debt which must be repaid. There are much fewer and lower barriers to obtaining and using a credit card than there are to obtaining, for example, a mortgage. As such, there are some drawbacks both in terms of typically higher interest rates, as well as some structural differences.

Example 2.4.6.

Bilqis gets a credit card, with 17.99% APR compounding daily. She uses the card to buy a $900 plane ticket. She does not make any payments during the interest-free grace period. Her first payment is due 35 days after the grace period ended. Following the fine print in the credit card agreement, the minimum payment is calculated to be 1% of the outstanding balance after applying the APR; or $25, whichever is larger. What is her outstanding balance? What is her minimum payment? If she pays the minimum payment what will her new balance be?

Solution.

First we will see what she owes with the 17.99% APR using the compound interest formula for 35 days:

\begin{equation*} 900\left(1+\frac{0.1799}{365}\right)^{35} \approx 915.66 \end{equation*}

The spreadsheet formula for this computation is

=FV(0.1799/365,35,0,900)

With interest, Bilqis now owes $915.66.

Now we will find one percent of the new balance which is

\begin{equation*} \$915.66(0.01) \approx \$9.16 \end{equation*}

$25 is larger than $9.16, so her first payment must be at least $25. If she makes the minimum payment we can subtract to find her new balance:

\begin{equation*} \$915.66-\$25 = \$890.66 \end{equation*}

Her new balance will be $890.66.

Subsection 2.4.5 Summary of Spreadsheet Formulas

Here are all the spreadsheet formulas from this chapter so far together so you can see the similarities and differences.

Spreadsheet Formulas.

=principal+principal*rate*time

=FV(rate per period, number of periods, payment amount, present value)

=principal*EXP(yearly rate*years)

=PV(rate per period, number of periods, payment amount, future value)

=PMT(rate per period, number of periods, present value, future value)

=EFFECT(stated rate, number of compounding periods per year)

rate per period: is the interest rate per compounding period, $r/n$
number of periods: is the total number of periods, $n*t$
payment amount: is the amount of regular payments, $d$
present value: is the amount deposited or principal, $P$
future value: is the amount you want in the future, $0$ for a loan

Subsection 2.4.6 When to use each spreadsheet formula: What is the question asking?

Find a payment: =PMT
Find the effective rate or compare accounts: =EFFECT
How much do you need to deposit now, what loan amount can you afford, or remaining loan balance: =PV
What will the account balance be in the future?
- Simple interest: =principal+principal*rate*time
- Compound interest (except continuous): =FV
- Continuously compounded interest: principal*EXP(rate*years)

Subsection 2.4.7 Summary of Mathematical Formulas

Mathematical Formulas.

Simple Interest

\begin{equation*} I=Prt \text{ or } A=P+Prt \end{equation*}

Compound Interest

\begin{equation*} A=P\left(1+\frac{r}{n}\right)^{nt} \text{ or } P=\frac{A}{\left(1+\frac{r}{n}\right)^{nt}} \end{equation*}

Continuously Compounded

\begin{equation*} A=Pe^{rt} \text{ or }P=\frac{A}{e^{rt}} \end{equation*}

Savings Plans

\begin{equation*} A=\frac{d\left(\left(1+\frac{r}{n}\right)^{nt}-1\right)}{\left(\frac{r}{n}\right)} \text{ or } d=\frac{A\left(\frac{r}{n}\right)}{\left(\left(1+\frac{r}{n}\right)^{nt}-1\right)} \end{equation*}

Loans

\begin{equation*} P=\frac{d\left(1-\left(1+\frac{r}{n}\right)^{-nt}\right)}{\frac{r}{n}} \text{ or } d=\frac{P\left(\frac{r}{n}\right)}{\left(1-\left(1+\frac{r}{n}\right)^{-nt}\right)} \end{equation*}

$P$: is the principal, starting amount, or present value
$d$: is your loan payment (your monthly payment, annual payment, etc.)
$r$: is the annual intrest rate in decimal form
$n$: is the number of compounding periods in one year
$t$: is the length of the loan, in years
$A$: is the end amunt or future value

If the compounding frequency is not always explicitly given, it is determined by how often you make payments

Subsection 2.4.8 When to use each mathematical formula: What is the question asking?

Find a payment
- Savings payment: savings plan equation (positive exponent) solved for $d$
- Loan payment: loan equation (negative exponent) solved for $d$
How much do you need to deposit now?
- Compound interest (except continuous): compound interest formulas solved for $P$
- Continuously compounded: the formula with e solved for $P$
What loan amount can you afford, or remaining loan balance: loan formula solved for $P$
What will the account balance be in the future?
- One-time deposit:
  - Simple interest: simple interest formula
  - Compound interest (except continuous): compound interest formula solved for $A$
  - Continuously compounded interest: the formula with $e$ in it, solved for $A$
- Regular payments: Savings plan formula solved for $A$

Remember, the most important part of answering any kind of question, money or otherwise, is first to correctly identify what the question is really asking, and to determine what approach will best allow you to solve the problem. After practicing with the exercises from this section, you can test yourself on which formula to use with exercises 14-21.

Exercises 2.4.9 Exercises

1.

You can afford a $700 per month mortgage payment. You’ve found a 30-year loan at 5.5% APR.

How big of a loan can you afford?
How much total money will you pay the loan company?
How much of that money is interest?

2.

Marie can afford a $250 per month car payment. She’s found a 5-year loan at 7% APR.

How expensive of a car can she afford?
How much total money will she pay the loan company?
How much of that money is interest?

3.

You want to buy a $25,000 car. The company is offering an interest rate of 2% APR for 48 months (4 years). What will your monthly payments be?

4.

You decide to finance a $12,000 car at 3% APR compounded monthly for 4 years. What will your monthly payments be? How much interest will you pay over the life of the loan?

5.

You want to buy a $200,000 home. You plan to pay 10% as a down payment and take out a 30-year loan for the rest.

How much is the loan amount going to be?
What will your monthly payments be if the interest rate is 5%?
What will your monthly payments be if the interest rate is 6%?

6.

Lynn bought a $300,000 house, paying 10% down, and financing the rest at 6.5% APR for 30 years.

Find her monthly payments.
How much interest will she pay over the life of the loan?
What percentage of her total payment was interest?

7.

Emile bought a car for $24,000 three years ago. The loan had a 5-year term at 3% APR. How much does he still owe on the car?

8.

A friend bought a house 15 years ago, taking out a $120,000 mortgage at 6% APR for 30 years. How much does she still owe on the mortgage?

Exercise Group.

Use a spreadsheet (not formulas) to answer problems 9 through 13 below.

9.

Imagine you have $20,000 saved as a down payment on a house. You wish to take out a fixed-rate 30-year mortgage loan at 4% APR (remember that mortgage rates usually assume monthly compounding). If the maximum mortgage payment you can afford is $950 per month, then what is the maximum house price that you can afford?

10.

Suppose another mortgage lender offers you a fixed-rate 15-year mortgage at 2.95% APR. You have $20,000 saved as a down payment, and you can afford a maximum mortgage payment of $950 per month. You are interested in a certain house for sale, with firm selling price of $200,000.

Find the monthly payment for this house. Can you afford it, under the terms of this lender?
(Challenge): Suppose this same lender offers to increase the APR by only 0.05%, for each additional year added to the loan period beyond 15 years (so that a 16-year loan would have 3.00% APR, and a 17-year loan would have 3.05% APR, and so on), up to a maximum loan period of 25 years. Given these terms, does any combination of APR and loan period exist that would let you afford the house? If so, state the minimum number of additional years needed, the total resulting loan period, the resulting APR, and the resulting monthly payment.

11.

An annuity firm pays 5% APR compounded yearly, and offers an investor the following: Deposit $100,000 with them today, and then starting one year from today, you will receive ten equal annual payments, with zero balance remaining afterward in the account. If an investor accepts their offer, then find the following:

What will be the payment amount for each of the ten equal payments?
After ten years, how much interest will the investor have received, and what percentage of the total payment sum will represent interest?

12.

For twelve full years, and into an account that pays 3.5% APR compounded quarterly: Yanhong will either pay $1500 at the end of each calendar quarter, or, deposit a single lump sum that will give the same future value amount.

If Yanhong chooses the single lump sum option, then how much will Yanhong need to deposit?
If Yanhong needs to have earned $100,000 in this account at the end of the twelve years, then the quarterly deposit amount will need to be increased. What would the new quarterly deposit amount need to be?
(Challenge): If Yanhong will make quarterly deposits into this account for the twelve years, but also has $8,000 to additionally deposit into this account right away: What would the new quarterly deposit amount need to be, so that the total balance after twelve years is $100,000?

13.

Assume you take out a 30-year mortgage loan for $250,000 at a fixed 4.5% APR.

What will be the amount of your monthly payment?
After the first ten years of payments, how much will remain on your loan balance?
After the first twenty years of payments, how much will remain on your loan balance?
Notice that the amount of the loan balance reduction during the second ten years, was very considerably bigger than the amount of the loan balance reduction during the first ten years. Why does the loan balance decrease at a faster and faster pace, the longer that the loan has been in repayment?

Exercise Group.

For each of the following scenarios, determine which formula from sections 2.2-2.4 to use and solve the problem.

14.

Keisha received an inheritance of $20,000 and invested it at 6.9% APR, compounded continuously. How much will she have for college in 8 years?

15.

Paul wants to buy a new car. Rather than take out a loan, he decides to save $200 a month in an account earning 3.5% APR compounded monthly. How much will he have saved up after 3 years?

16.

Sol is managing investments for a non-profit company. They want to invest some money in an account earning 5% APR compounded annually with the goal to have $30,000 in the account in 6 years. How much should Sol deposit into the account?

17.

Miao is going to finance new office equipment at 2.8% APR over a 4-year term. If she can afford monthly payments of $100, how much equipment can she buy?

18.

How much would you need to save every month in an account earning 4.1% APR to have $5,000 saved up in two years.

19.

Terry and Jess are buying a house for $405,000 and they can afford to put 10% down. Their interest rate is 4.3% APR for 30 years. What will their monthly mortgage payment be?

20.

You loan your sister $500 for two years and she agrees to pay you back with 3% simple interest per year. How much will she pay you back

21.

Zahid starts saving $150 per month in an account that pays 4.8% APR compounded monthly. If he continues for 20 years, how much will he have? If he waited 10 years instead and put in $300 per month for 10 years with the same interest, how much would he have?

Prev Top Next