Objectives
Students will be able to:
- Perform basic calculations on a spreadsheet
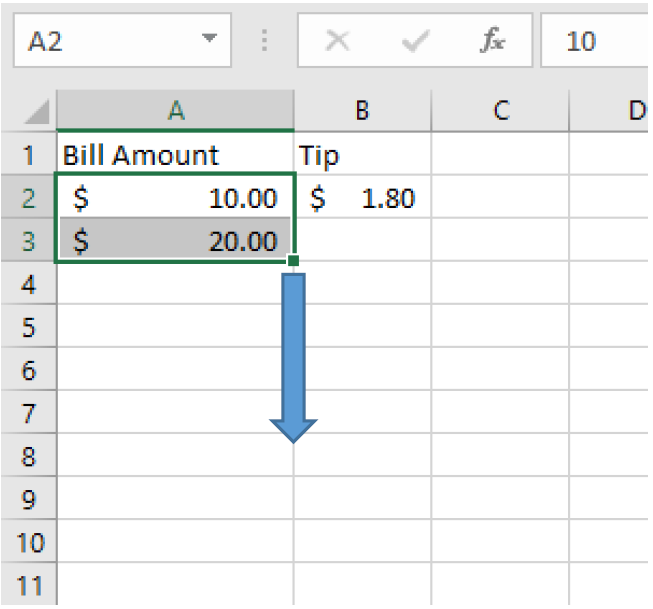
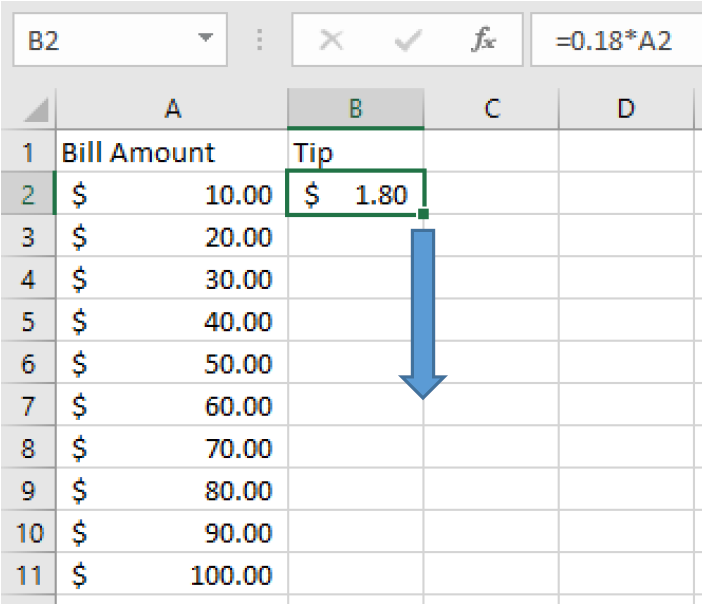
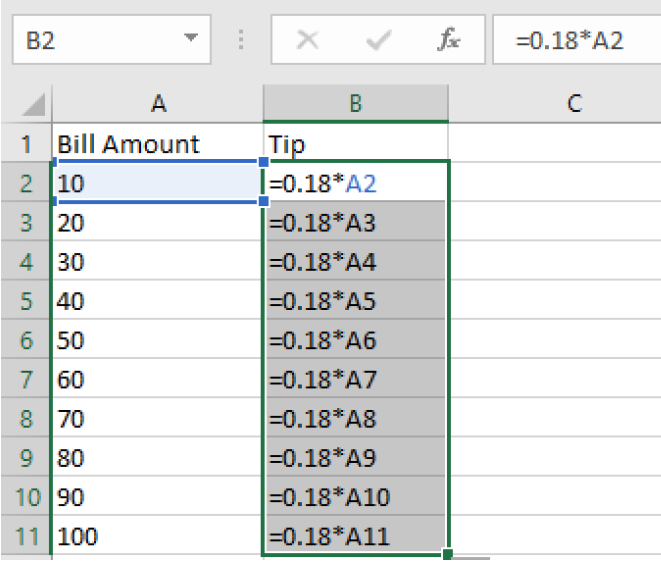
- Use cell references and the fill-down feature
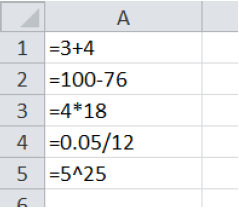
=3+4
=100-76
=4*18
=0.05/12
=5^25
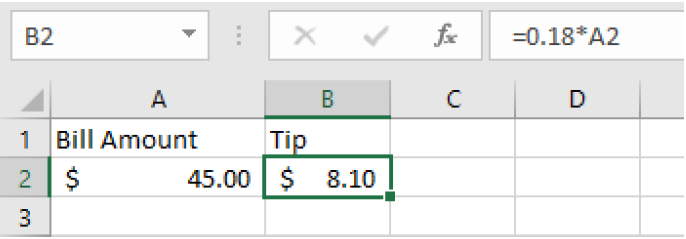
=0.18*35.75
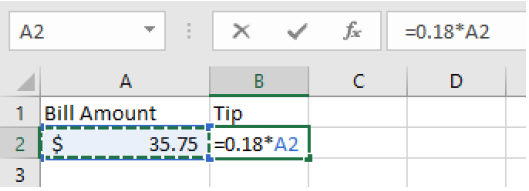
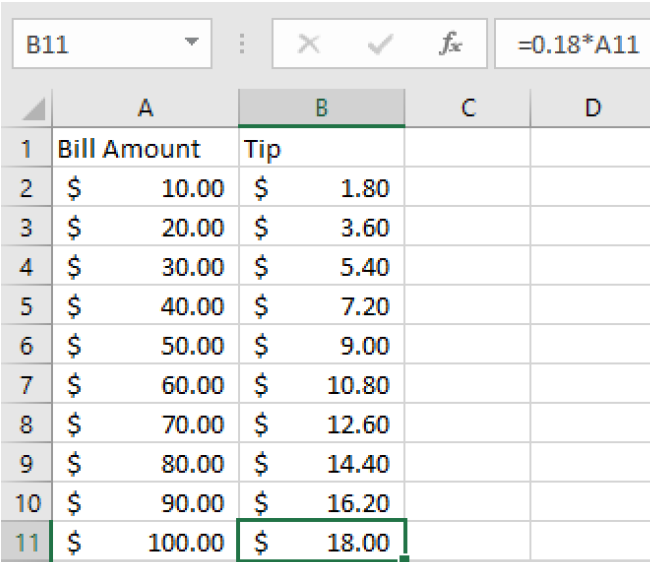
=0.18*A2
=FV to calculate the future values of an investment=PV to calculate the deposit needed for a desired future balance=PMT to calculate a loan or savings plan payment=EFFECT to calculate the effective rate of an account and compare accounts= 1000 * (103%) * (103%). Perform this computation in a spreadsheet and write the balance that you find.= 1000 * (103%)^2. Notice that the result here, which involves using a power, gives the same answer as you found in part (a). Comparing the two spreadsheet computations: Explain why they give the same result.